Marie has one regular die labeled with the numbers 1, 2, 3, 4, 5 and 6 and a second cube that is completely blank. She labels this cube in a special way. If you roll both dice, you can get the following totals: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. The special part: all 12 total values are equally likely to be rolled. How did Marie label the cube?
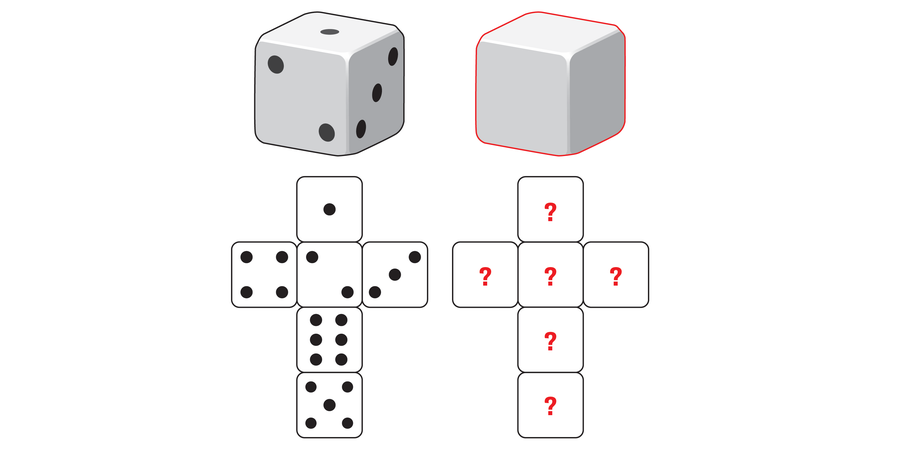
The sides of the die must be labeled 0, 0, 0, 6, 6 and 6.
There are 36 possible totals when rolling two dice. If the 12 sum values are all to have the same probability, then each value must occur exactly three times.
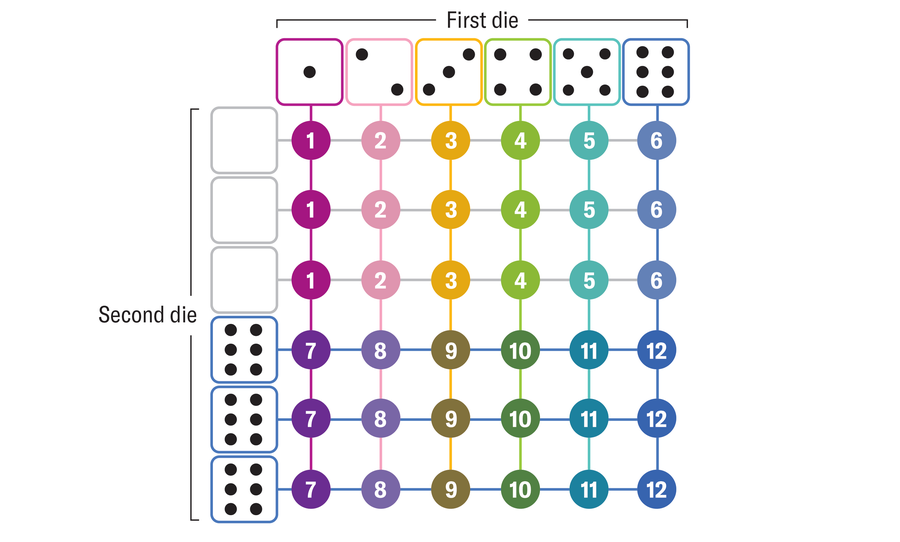
The total value of 12 can be achieved with two dice only if both dice show a 6. Because the value 12 must appear three times in the table, the cube Marie labels must have three sides with a 6. The rest of the needed results are possible only if the other three sides are labeled with a 0.
For each sum value from 1 to 12, the probability p is
p = 3 / 36 = 1 / 12 ≈ 8.3%
We’d love to hear from you! E-mail us at games@sciam.com to share your experience.
This puzzle originally appeared in Spektrum der Wissenschaft and was reproduced with permission.





